作者:孟憲川(南京大學建築與城市規劃學院)原文刊載於《建築學報》2019年6期
彎矩,英文「bending moment」,是一個抽象的力學概念,指構件在外力作用下受彎時,構件內部產生的一種抵抗內力,它伴隨著17世紀現代結構工程專業的產生而出現。
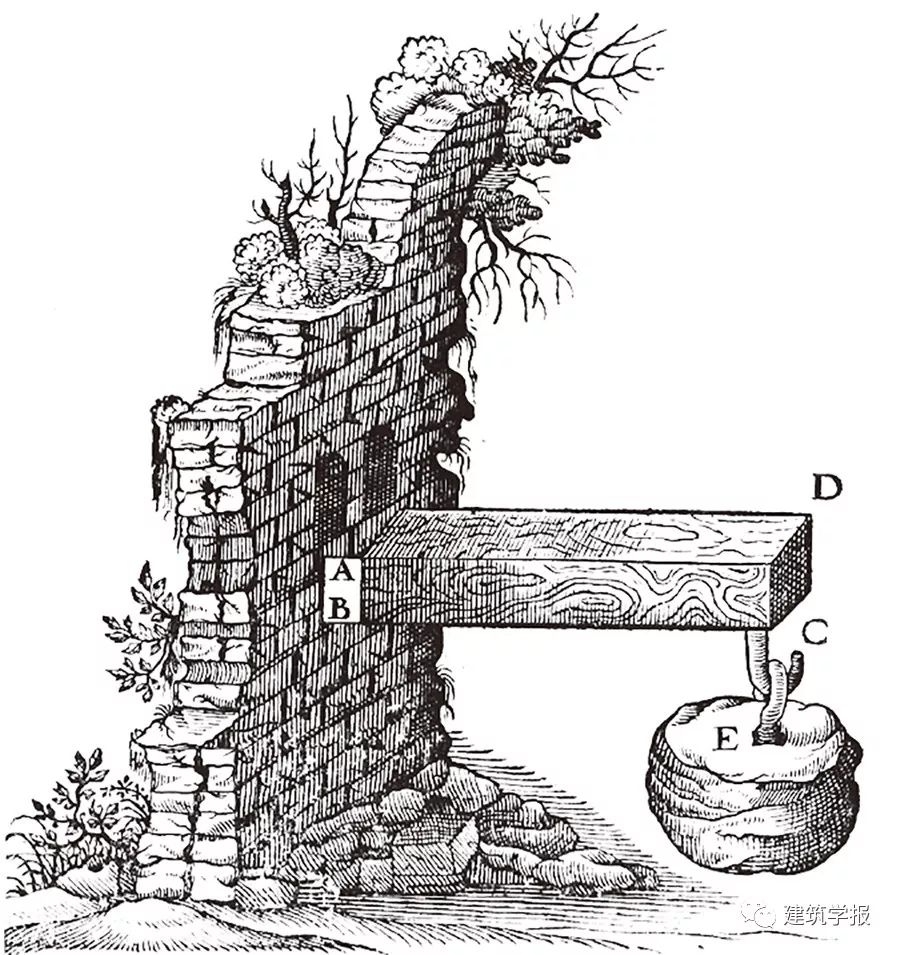
對彎矩的科學認知始於1683年伽利略(Galileo Galilei,1564-1642)在《關於兩種新科學的對話》中描述的懸挑梁實驗(圖1)——雖然結論有誤,完善於1826年克勞德-路易‧納維(Claude-Louis Navier,1785-1836)以彈性理論為基礎的微分方程——截面慣性矩和材料彈性模量直接影響彎矩。
然而結構工程專業與建築設計的獨立發展導致建築與結構之間的隔閡一直存在,逐漸形成結構後合理化(post rationalization)的設計方法。二者的分離常帶來設計不合理、造價高昂等現象。
在探索建築形式語言和追求結構性能並重的趨勢中,建築與結構的整合設計愈發重要。「建築-結構」一體化設計,即權衡設計各方因素,促使滿足建築需求的形態與符合結構受力的形態相互趨近,選取適合項目的、建築與結構融合姣好的形態。
彎矩,是建築師與結構師可溝通的為數不多的概念。基於彎矩圖的建築創作方法是建築-結構一體化設計方法之一,本文嘗試以彎矩圖為基礎,由整體到局部,從形態、構件、節點各方面,逐一借助案例揭示彎矩圖激發建築創作的潛在可能。
1 由結構走向建築的彎矩
彎矩自1826年至今約200年時間裡被結構分析反覆使用,卻沒有從輔助結構分析廣泛走向激發建築設計。解決這個問題至少需兩方面思考:使用彎矩的方式和方法。
1.1 從公式到圖示
公式是結構量化分析的基石,彎矩也不例外。在與彎矩相關的諸多公式中,彎矩是力與距離的乘積,也是連續荷載力矩的積分;透過確定斷面慣性矩、應力到中性軸的距離,彎矩與構件最大應力的關係可被量化;藉由確定受彎截面的慣性矩與材料的彈性模數,彎矩與構件撓度的關係可以被量化等。上述公式說明彎矩與尺寸、構件、材料發生著密切關係。然而,要求建築師將公式直接轉化為設計靈感卻著實困難,因為圖示才是建築師的思考方式。
彎矩公式是科學家對實際受力形態的簡化與抽象,以便被廣泛使用。當公式再次轉化為有規律的圖示時,極大地幫助建築師理解結構受力形態,增加了建築-結構一體化創作的可能。圖2以一段承受均布荷載的簡支梁為例,簡支梁變形圖示直觀表達撓度概念,彎矩圖呈現連續荷載作用下力矩幾何形狀,變形斷面圖示揭示材料壓拉狀態等。本文同時使用精確繪製的定量彎矩圖和快速繪製的定性圖示,二者在文中統稱為彎矩圖。
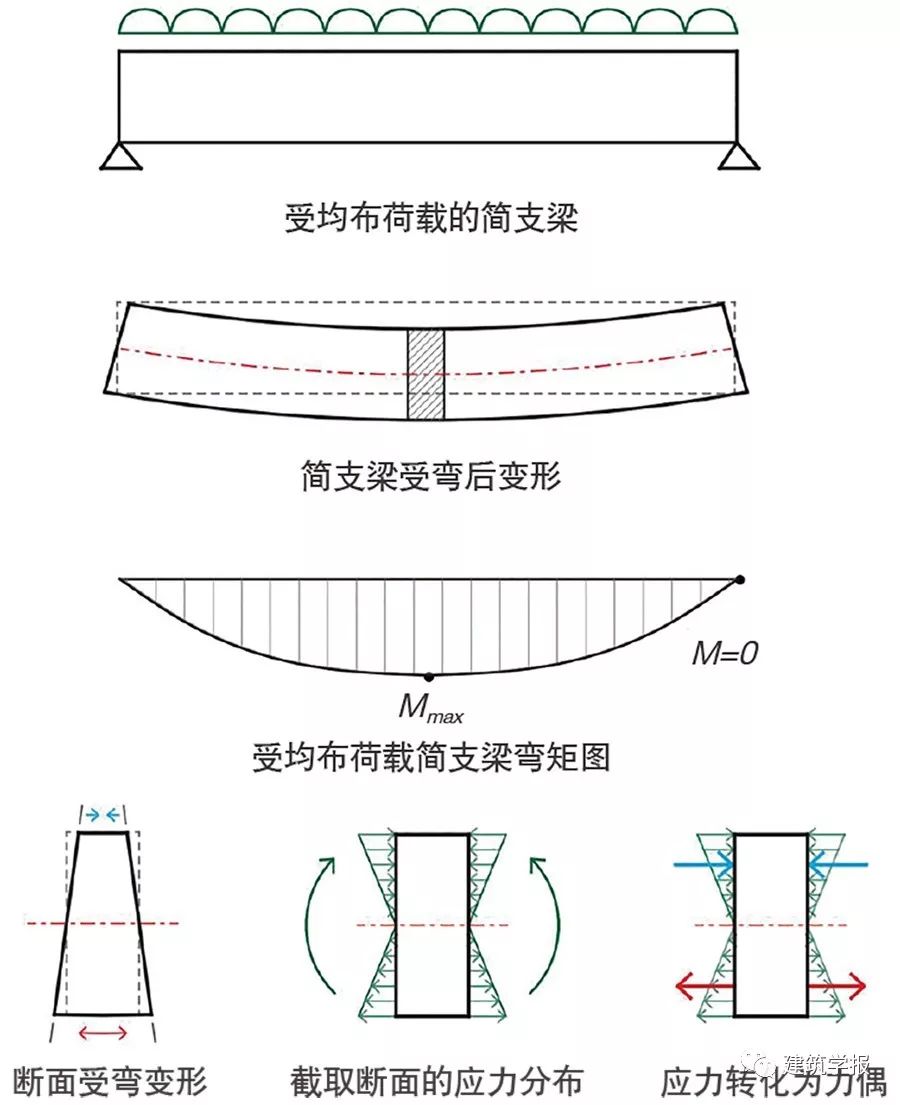
透過彎矩圖,構件變形、應力分佈、拉壓情況被一一呈現,可直接融入形態操作過程,因此彎矩圖是幫助建築師展開創作的方式。
1.2 彎矩圖的使用方法
建築形態符合彎矩圖使結構性能良好是不言而喻的共識,該共識潛意識地傳遞了彎矩圖的建築-結構一體化設計方法:將彎矩圖的輪廓直接套用於建築形態。相同邏輯的設計方法常用於橋樑設計,很多結構輕盈、造型雅緻的橋與其彎矩圖線條所呈現的輪廓高度一致。該方法用於建築設計時則存在一定風險,甚至有某些作品的結構技師聲稱自己才是真正的首席設計師。這也是不少建築師對該方法的疑慮所在,因為結構性能最高效很少是建築設計的唯一選項。
將彎矩圖輪廓直接作為建築形態有待商榷,但並不意味著全面否定該方法。以其為基礎稍作調整,能為建築形態創作帶來新思路:通過綜合權衡建築與結構因素得到非均布荷載,可獲得特定結構形態,例如滑鐵盧國際車站;基於彎矩圖與傳力路徑的轉換,操作彎矩圖內部,在結構形態輪廓內滿足建築需求,例如比利時克諾克人行橋;綜合權衡結構與建築因素,調整彎矩圖輪廓使結構形態符合空間要求,例如巴黎蓬皮杜中心。
上述案例的建築形態是對彎矩圖的直觀呈現,並不適合絕大多數建築項目。本文旨在從形態、構件、節點三方面,為廣大建築設計實踐提供多種彎矩圖使用方法,為建築師揭示基於彎矩圖的建築-結構一體化設計方法。
2 彎矩圖與形態
在建築師與結構師的合作中,通過將彎矩圖轉譯為建築形態設計中可靈活操作的設計要素,使彎矩圖更廣泛服務建築設計。本文梳理了三種具體手法:摺疊界面,平滑曲面和避讓空間。
2.1 摺疊界面
基於反彎點彎矩為零、上下傳力的原理,對彎矩圖進行摺疊操作,獲得符合結構需求的、連續轉折的建築界面。
瑞士庫爾城市媒體中心(Stadthaus und Medienzentrum)地處路口轉角(圖3),為了呼應基地周邊老建築和滿足現代辦公,瑞士建築師托馬斯‧哈斯勒(Thomas Hasler)採用鋼筋混凝土結構,並將立面設計為巨大而純淨的矩形玻璃窗。
為創造連續開放的戶外公共空間,建築師儘可能減少建築底層支座數量,在展開立面中除兩端設置支撐外,在跨中保留三顆非轉角立柱,形成轉角開敞的城市空間,其中最大懸挑約17公尺。
面對該懸挑巨大且不許設置斜撐的鋼筋混凝土結構,結構師於爾格‧康策特(Jurg Conzett)分別用格貝梁——由海因里‧格貝(Heinrich Gerber,1832-1912)1866年發明的跨中鉸接的梁——回應巨大懸挑,用范倫第桁架(Vierendeel Truss,弗倫第爾桁架、空腹桁架)——由亞瑟‧弗倫第爾(Arthur Vierendeel,1856-1940)1898年發展出的空腹桁架——回應巨大窗洞 。
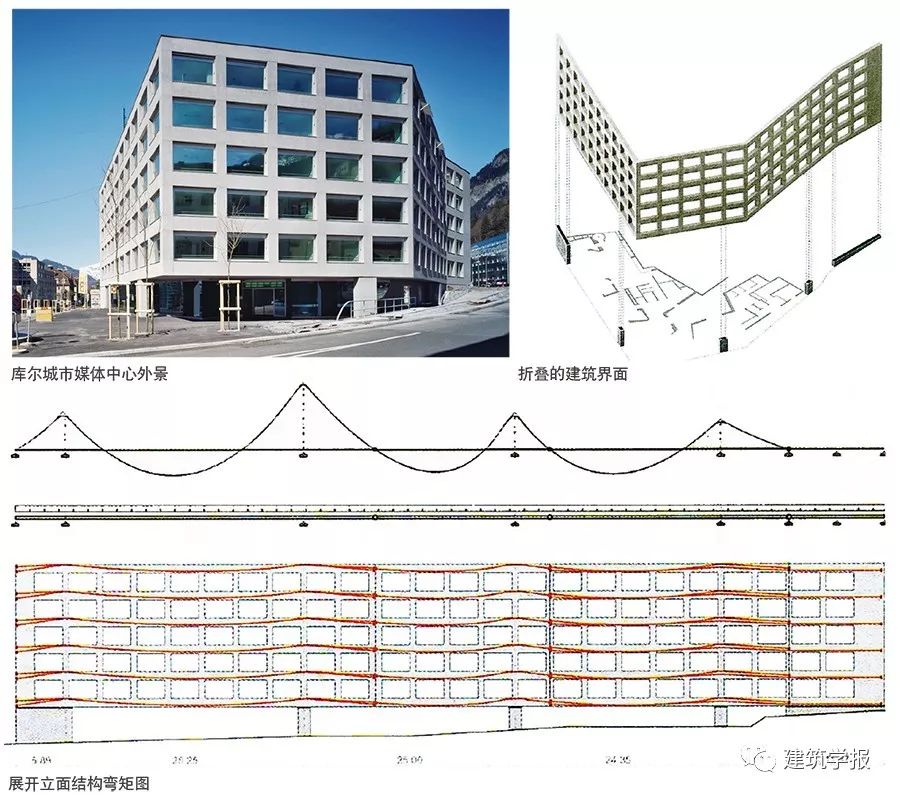
然而,康策特並非直接使用格貝梁,而是首先將平面內連續格貝梁如摺紙般折成三段,形成設計所需的三維城市界面。轉折點的選取非常講究——格貝梁的均布荷載彎矩圖的跨中反彎點,反彎點意味著彎矩從一端經過該點通向另一端時,截面的拉壓應力屬性發生反轉,且該點彎矩為零,從理論角度講該點只在垂直方向傳力。為滿足懸挑尺度,康策特選擇預應力技術,埋置的預應力鋼索形態與格貝梁彎矩圖受拉側曲線一致,設置在每層窗下牆到梁底之間約1m高的外梁中,既滿足樓板結構梁小淨空大的建築需求,又滿足造型的結構需求。
2.2 平滑曲面
基於反彎點彎矩為零、變形更小的原理,將一系列彎矩圖反彎點連接成線,從受力角度控制建築曲面形態的平滑程度。
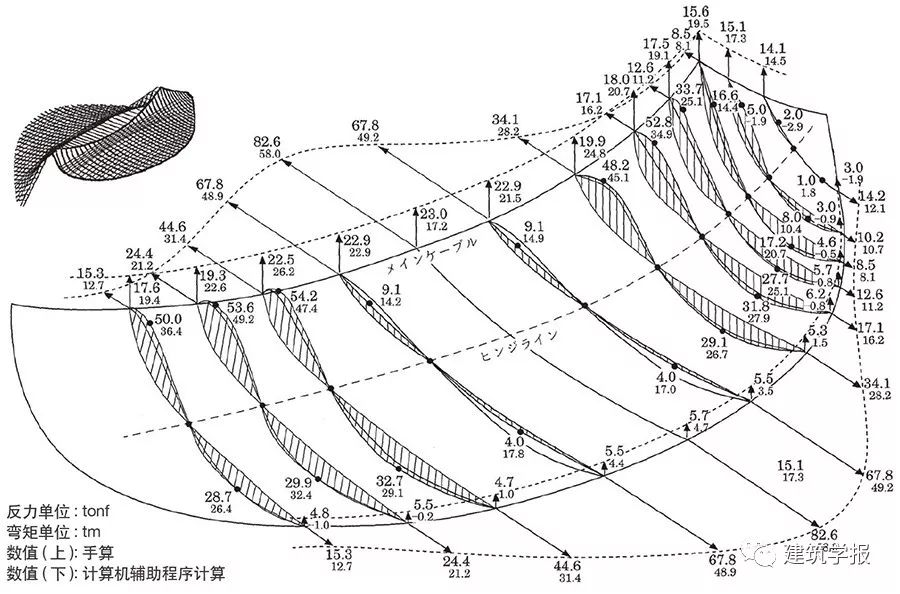
日本國立代代木體育館第一場館由丹下健三設計(圖4)。建築在形態設計中將日本傳統建築樣式與結構高度融合,被認為是跨時代作品,丹下健三將這個作品的突破點描述為,創造在競技時刻將所有的運動員與觀眾共聚一堂的建築,挑戰前所未有的懸索結構。屋面由跨度126m的鋼索作為屋脊,再從屋脊向兩側懸掛鋼樑形成三維曲面,鋼樑的最大跨度約60m。
構成曲面的構件是截面高度不同的工字型鋼樑,鋼樑翼緣尺寸為22mm×190mm、腹板厚度為12mm、截面高度變化於0.5~1m之間。懸掛的工字鋼不是懸索結構,而是半剛性懸掛結構,存在彎矩。為保證建築三維曲面的優雅過渡,項目結構師川口衛通過手算,得到每榀懸掛工字鋼樑的固定荷載彎矩圖,將一側屋面所有鋼樑的反彎點依次連接成線,該連線在曲面過渡的轉折處,是控制三維曲面形態的關鍵曲線,確保該控制曲線舒展,就能從結構角度保證三維曲面形態過渡平滑。
2.3 退讓空間
基於彎矩圖可彎折原理,避讓出建築設計中所需要的空間,得到滿足建築設計需求的合理結構系統。
在日本熊本縣車站西口廣場中,建築師佐藤光彥為了創造將交通與行人柔性分割的廣場,設置了帶一系列洞口的薄牆,延續的屋頂為人們提供半室外公園般的舒適環境,但在這個高5m的半室外空間中,建築師期望立柱尺寸纖細,儘可能使行人忽略對立柱的關注(圖5)。
連續界面會因為風荷載形成水平力,同時需要考慮結構對水平地震力的抵抗效用。建築形態源於水平集中荷載作用下人字三角撐轉化而來的彎矩圖。該人字撐較為特殊,原來的一捺轉為豎直,成為不受彎矩的纖細立柱,原來的一撇則彎折成直角,成為承受彎矩的屋面與牆體復合結構。
由此,結構師小西泰孝將5m通高的柱徑限制在165.2mm,用100mm厚彩鋼板與6mm厚鋼板銲接成復合鋼板壁,用200mm×200mm×8mm×12mm的工字鋼做梁,鋼板壁與鋼樑形成可以傳遞彎矩的整體構件,解決了水平推力下整個建築的穩定問題。

3 彎矩圖與構件
彎矩圖與形態的關係在設計中最容易被觀察,然而,從彎矩發掘史可以清晰地說明,彎矩的被意識與被完善是針對單根懸挑構件的集中研究,因此,對比形態微觀的構件層面,彎矩圖有輔助局部設計的天然基礎。本文梳理了三種具體手法:均衡形力、規定構件和極致尺寸。
3.1 均衡形力
基於不同方案中彎矩圖和最大彎矩值的比選,權衡建築與結構需求,獲得建築設計與結構設計的融合。
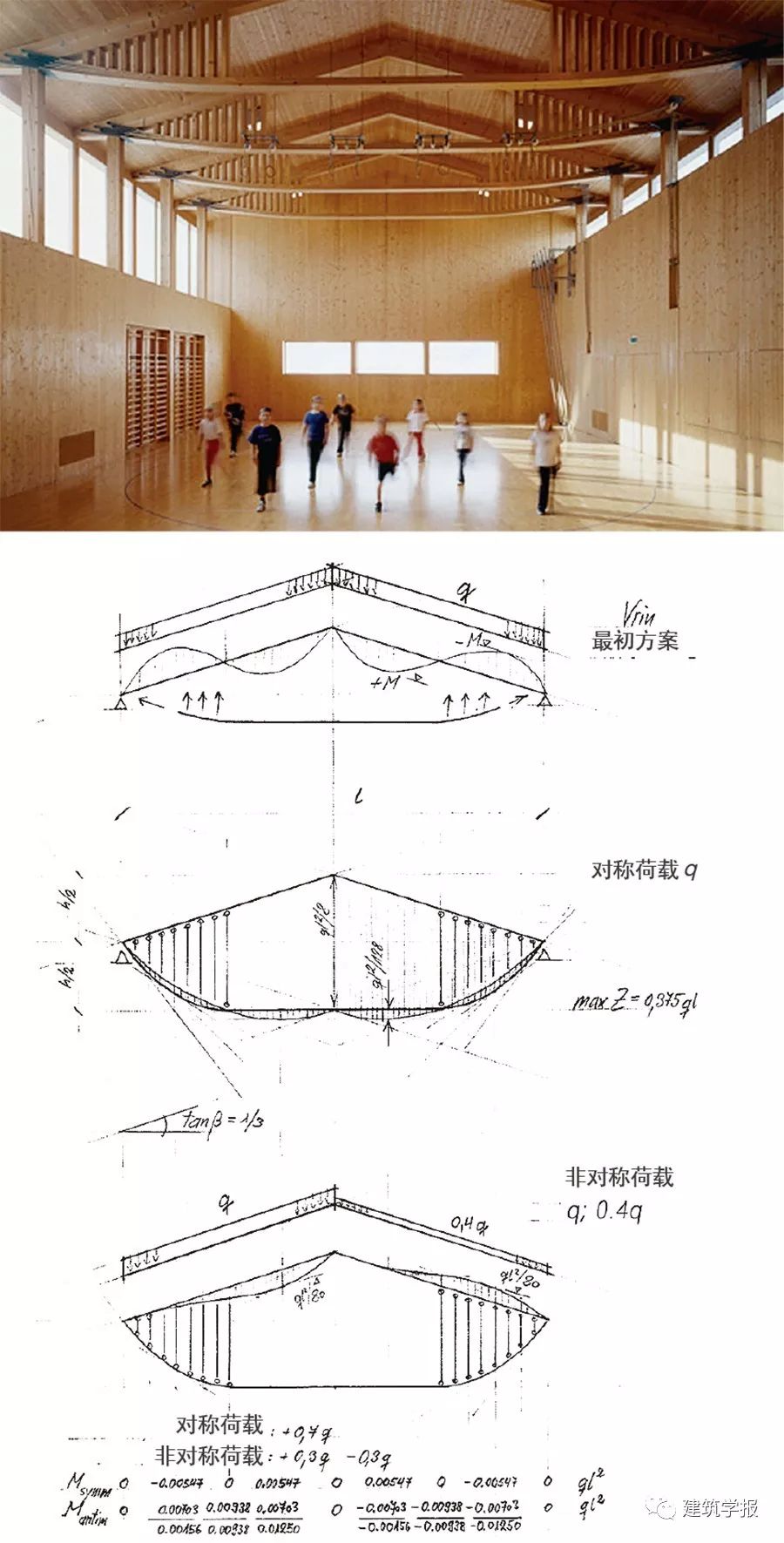
瑞士弗林多功能廳(Multipurpose Hall in Vrin)是當地建築師吉翁‧卡米納達(Gion Caminada)的代表作品之一(圖6),這個跨度11m的木房子從外觀看只是普通雙坡頂樑柱結構,但屋頂是建築形式語言創新的重點。康策特用彎矩圖推敲屋頂設計,他首先想到了羅伯特‧馬亞爾(Robert Maillart,1872-1940)設計的基亞索(Chiasso)倉庫屋架,並將其與典型三角屋架的非對稱荷載彎矩圖做比較,結論是基亞索屋架上弦材的最大彎矩只有典型三角屋架上弦材的1/3。
雖然基亞索桁架結構效率高效、構件尺寸小,但是該屋架尚不夠通透,因此康策特又提出了取消跨中豎桿、增加兩邊豎桿的設想。通過計算均布荷載時下弦材彎矩,以及非對稱荷載時上弦材彎矩,得到結論:新屋架下弦材彎矩很小,上弦材最大彎矩雖然比基亞索桁架增加了30%,但只為典型三角屋架的1/2,該形態權衡了建築與結構的需求。
屋架上弦材採用斷面為160mm×360mm的木料,下弦材選用5片斷面為300mm×24mm的帶狀板材組合而成,上下弦間壓桿的上下連接方式為榫卯。下弦與上弦的連接依靠特製的鐵板夾片,鐵板夾住下弦材並用直徑24mm的螺栓固定,再將夾板的彎折端鉸接於上弦材的螺栓上。整個屋架的設計,通過桿件彎矩圖的對比,在追求結構高效能的同時,並非執著於結構性能,而是在建築創作與結構效率之間取得平衡。
3.2 規定構件
基於相同尺寸構件不同彎矩圖的結構意義,利用規定構件組織結構體系以滿足建築空間需求。
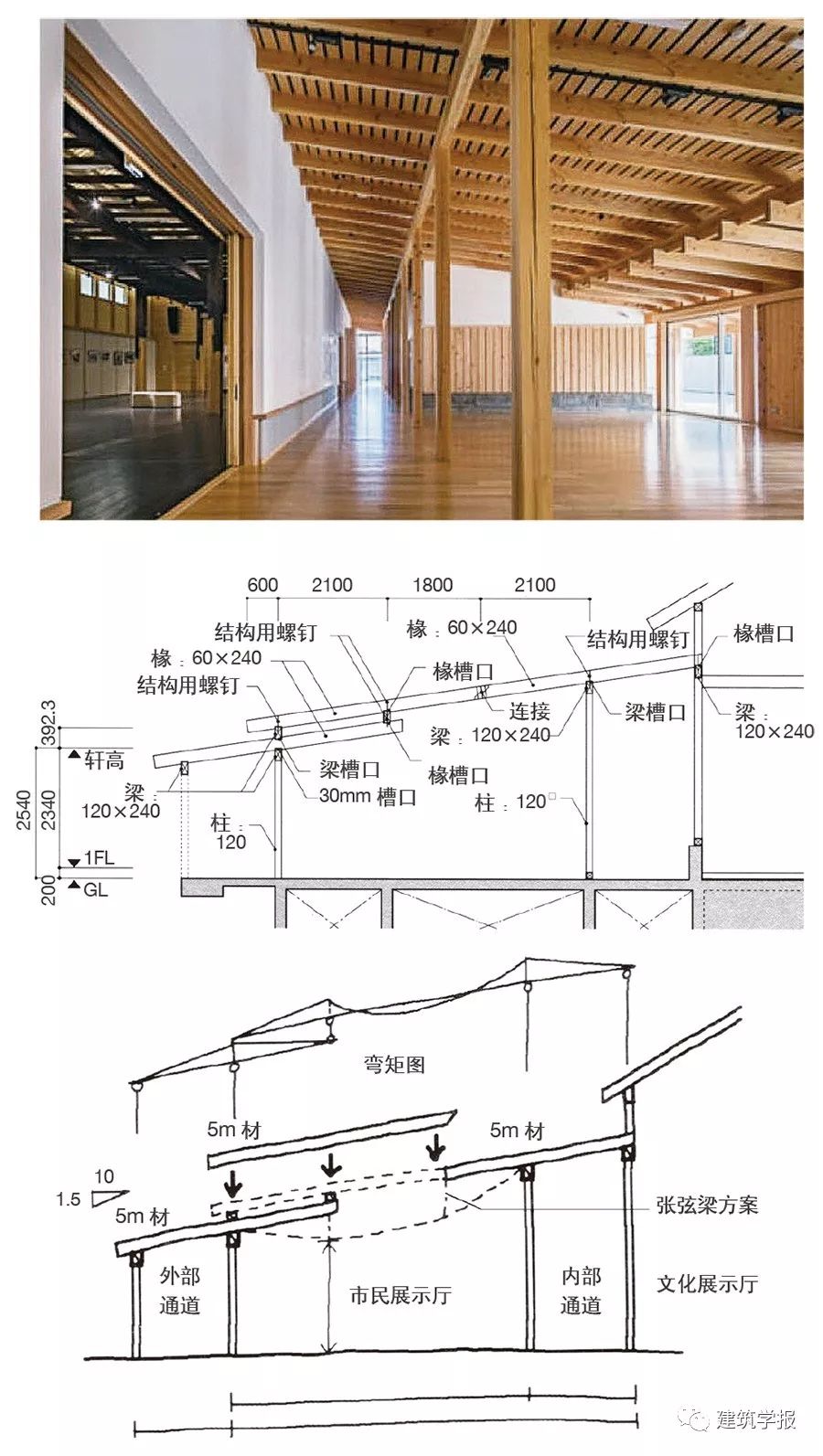
在日本茂木町文化交流館的市民展覽廳設計中(圖7),建築師內田雄文利用規定尺寸構件設計最大空間。市民展覽廳是緊鄰舊建築的單坡頂房間,平面尺寸為9.9×12.4m,從剖面看共三跨,中間最大跨為6m,但有一嚴格限制:結構梁的木枋為斷面60mm×240mm、長度5m的規格材。
針對該限制,結構技師山田憲明最初的想法是採用張弦梁,因為以簡支梁1/12的梁高跨度比推算,5m跨度尚需約420mm的梁高,張弦梁因在跨中增加支撐,使得梁彎矩相應減小,所需梁高隨之減小。然而該展廳屋頂的高度需低於現有老建築5m的簷口高度,導致張弦梁結構下淨高不滿足要求。
經多番思考,由於懸臂樑與格貝梁所需斷面尺寸比簡支梁小,山田憲明設計出兩端懸臂樑、中間疊加一段格貝梁的復合結構形式。在規定構件的前提下,彎矩圖輔助結構體系重組以滿足大空間需求。
3.3 極致尺寸
基於相同類型構件不同彎矩圖的結構意義,結合建築需求細分結構系統,獲得構件的極致尺寸。
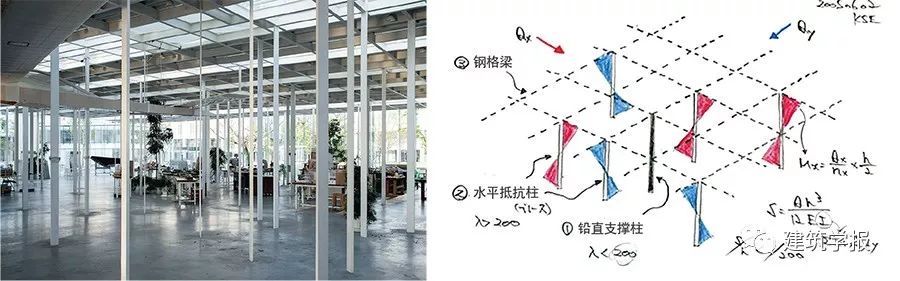
神奈川工科大學KAIT工坊是日本建築師石上純也探索建築極致尺寸的代表作之一(圖8)。在設計初期石上純也與結構師小西泰孝分享了纖細柱森林的想法,小西泰孝提出用扁鋼作為支撐的結構策略,為此提供使用扁鋼作為支撐的結構設計草圖,立柱被分為兩類:鉛直支撐柱和水平抵抗柱。草圖重點呈現了水平抵抗柱的受力問題,水平荷載被分成x軸(紅色)和y軸兩個方向(藍色),不同方向的水平抵抗柱各司其職。
小西泰孝為每根水平抵抗柱繪製彎矩圖,並在最右側紅色彎矩圖邊標記上彎矩公式,該公式的含義是水平向荷載被該方向立柱均分(QX/n),每根立柱的最大彎矩以柱高的一半計算(h/2) ——一般立柱頂部受水平力時彎矩值按照整個柱高計算,該公式意味著立柱頂端被設計為固端因而扁鋼寬度更小。處於結構極限狀態的框架通過減小柱距可獲得柱端彎矩。
但是,這種抵抗水平力的計算方法並沒有綜合考慮豎向力的作用,對極薄扁鋼而言,屋頂自重與積雪的豎向荷載會使其屈曲導致結構失效。為此,項目以預加載的施工方式,避免了扁鋼柱承受產生屈曲的豎向荷載。最終,在這座層高約5m、面積約2000㎡的建築中,林立著305根纖細鋼柱,鋼柱分兩種:42根抵抗豎向荷載的方鋼柱,截面厚度為55~62mm,寬度為80mm或90mm;263根抵抗水平向荷載的扁鋼柱,截面厚度為16~45mm,寬度為96~160mm。彎矩圖推動建築創作更細緻地推敲設計所需的極限形態。
4 彎矩圖與節點
相對於形態和構件,節點是更微觀的設計對象。彎矩圖直觀體現了構件與節點的關係:鉸接或剛接。前文案例中彎矩圖反彎點與鉸接點的對應關係就是形態設計的突破口之一。然而,對建築創作而言,設計最終關注的並非鉸接與剛接,而是與之對應的設計意義和具體做法。本文梳理了3種具體手法:補強拉壓,量化彎矩和迭代設計。
4.1 補強拉壓
基於彎矩圖拉壓關係與構造的聯繫,補強建築設計中結構較弱的部位,使項目更均衡地滿足建築與結構需求。
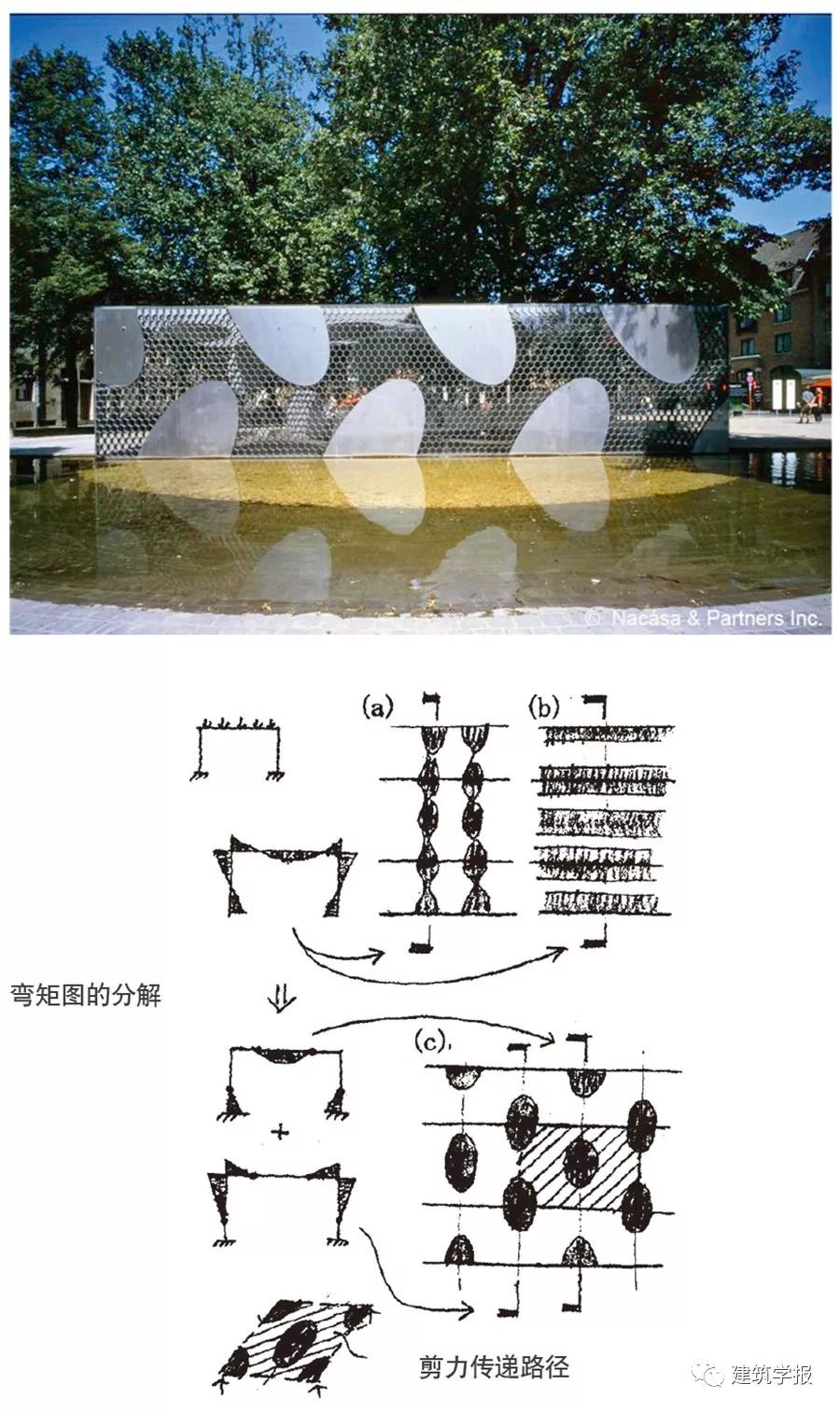
伊東豐雄設計布魯日展亭時有意選用鋁作為主材回應周邊中世紀的石砌建築,由此呈現布魯日城市中歷史感與現代感的共存(圖9)。伊東豐雄期望用鋁板蜂窩結構創造半透明的矩形管道,然而蜂窩板直接作為結構很容易變形。
為更加邏輯清晰地研究該作品,結構師新谷真人用拆解彎矩圖補強節點的方式幫助結構與建築更加有效地融合。新谷真人將15m×6m×3.5m的鋁結構展亭斷面抽象為矩形門框,綜合考量當地環境和建築功能後,得出雪荷載是影響結構最大因素的結論,因此以均布雪荷載為邊界條件得到腳部剛接的門式剛架彎矩圖,以此反向推敲設計所需的結構措施。
他曾考慮的措施是在蜂窩板外連續加上橢圓鋁板,通過增強拉力使整個結構能分別抵抗腳部、轉角和梁中的彎矩,進而接近剛架結構,然而該結構方式雖有效但形態不夠優雅。
於是,他將剛架彎矩圖一拆為二:梁中與腳部彎矩和只留轉角彎矩。前者構造措施是用一片鋁板解決梁中彎矩,半片鋁板解決一個腳部彎矩。後者構造措施是用一片彎折90º的鋁板滿足一個轉角彎矩所需的受拉構造。將前者與後者在空間上稍微錯開,既確保結構有效又形成優雅圖案,由此融合建築設計與結構設計。
4.2 量化彎矩
基於應力與彎矩之間可轉換原理,使構造的受力狀況可被量化,達到傳統節點的設計可控。
中國傳統木結構榫卯節點的智慧不僅體現於加工和裝配,也體現於結構性能尤其是抗震問題。日本傳統木構建築受中國唐代木構建築影響深遠,保留並發展出許多相似的榫卯節點。
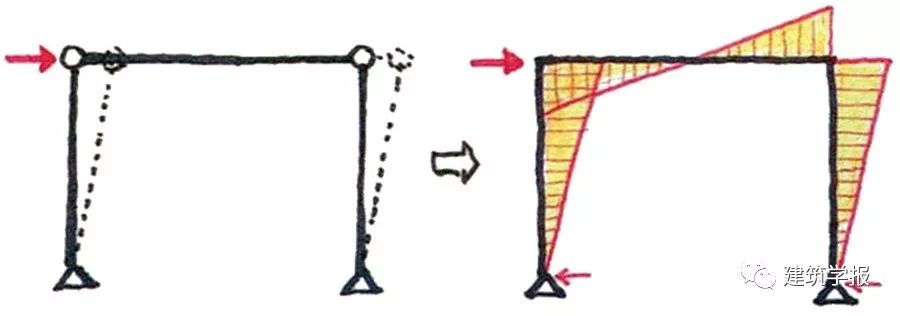
齋藤公男用鉸接框架與門式剛架的差別簡要說明了傳統木結構抗震的力學原理——剛架肩部的彎矩是抵抗水平力的秘密(圖10),他解釋到在海風、地震等水平力的作用下,原本不穩定的木構架很容易倒塌,但穿梁、楔子等構造增加了整個木架構的剛度,形成半剛性節點。對此,更準確的說法是,榫卯的構造方式產生彎矩。
四層傳統木結構的大洲城天守閣拆除於1888年,但該建築的雛形模型與外觀照片被保存下來,在當地政府的推動下,這座高19.5m的閣樓得以復原(圖11)。
由於與其他材料結構相比,傳統木結構榫卯節點對結構剛度和整體特性的影響更大,所以在項目展開的過程中,結構師山田憲明最關心的是傳統木結構節點的定量問題,並最終選用了稻山正弘的傳統木節點計算模型。
山田憲明將天守閣重要的樑柱節點分為三大類:貫通橫木,橫木穿過立柱且只有榫卯連接;長梁頭榫,梁穿過柱表面露出梁頭,除榫卯外在柱外部分加木銷;平梁頭榫,梁貫通立柱但不超出柱表面,除榫卯外在梁與柱交接處加木銷。
針對每類節點,山田憲明量化了產生彎矩的應力:貫通橫木的彎矩產生於榫卯轉動時木材擠壓的應力和界面錯動的摩擦力,長梁頭榫和平梁頭榫的彎矩來自於木材擠壓的應力、木銷的阻力和界面間的摩擦力。圖示一方面詳細揭示了榫卯節點中彎矩的來源,另一方面量化了榫卯節點的轉動剛度。
這也是山田憲明在此後實踐中對日本傳統木結構從繼承到創新的重要基礎。這裡使用的圖示是與彎矩圖直接相關的截面應力圖。詳解構造中彎矩產生原因、量化彎矩大小的圖示方法,對中國鄉村建設中木結構建築的傳承與創新有積極的參考意義。

4.3 迭代設計
基於彎矩圖與構造中不同做法的關係,為滿足特定結構目標持續改進構造,達到設計的優化迭代。
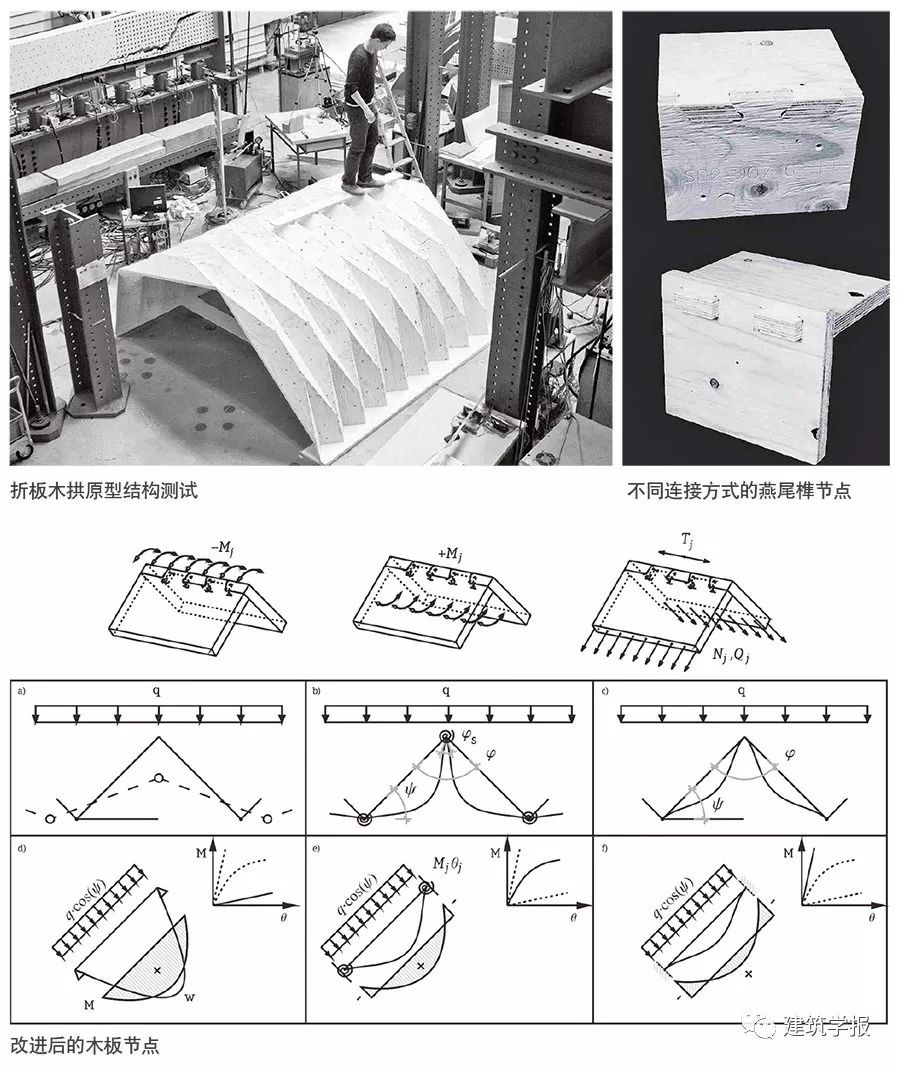
複雜形態不一定能直接使用彎矩圖輔助設計,但節點部位可借助彎矩圖展開討論。燕尾榫是兩片木板端部交接時,為防止節點受力脫開、企口為燕尾狀梯形的構造。在傳統工藝裡燕尾榫多用於不受外力的側角,很少用於承受荷載的頂部。折板拱接縫所使用的燕尾榫屬於後者。
在瑞士聯邦洛桑理工大學(EPFL)的折板木拱原型計畫(圖12)中,斯蒂芬‧羅氏(Stephane Roche)等人對折板的燕尾榫節點展開了圍繞彎矩圖的討論。折板的燕尾榫節點主要受正反向彎矩、板內軸力和折板脊部側力,折板拱榫卯連接可分為靈活的鉸接、抵抗部分彎矩的半剛接,和完全抵抗彎矩的剛接,與之相應的彎矩圖能夠顯示出同樣荷載下木板厚度越來越薄的趨勢。結構試驗證明了傳統燕尾榫節點抵抗彎矩的能力有限,為此他們在後續研究中發展出其他構造方式使節點儘可能抵抗彎矩。
5 結論
彎矩作為建築師與結構師之間為數不多的可溝通概念,應該打破結構後合理化方法中對分析與計算的過於專注,更廣泛地為建築-結構一體化的建築創作服務。彎矩服務建築設計具有可行性的關鍵是:彎矩圖的使用方法。
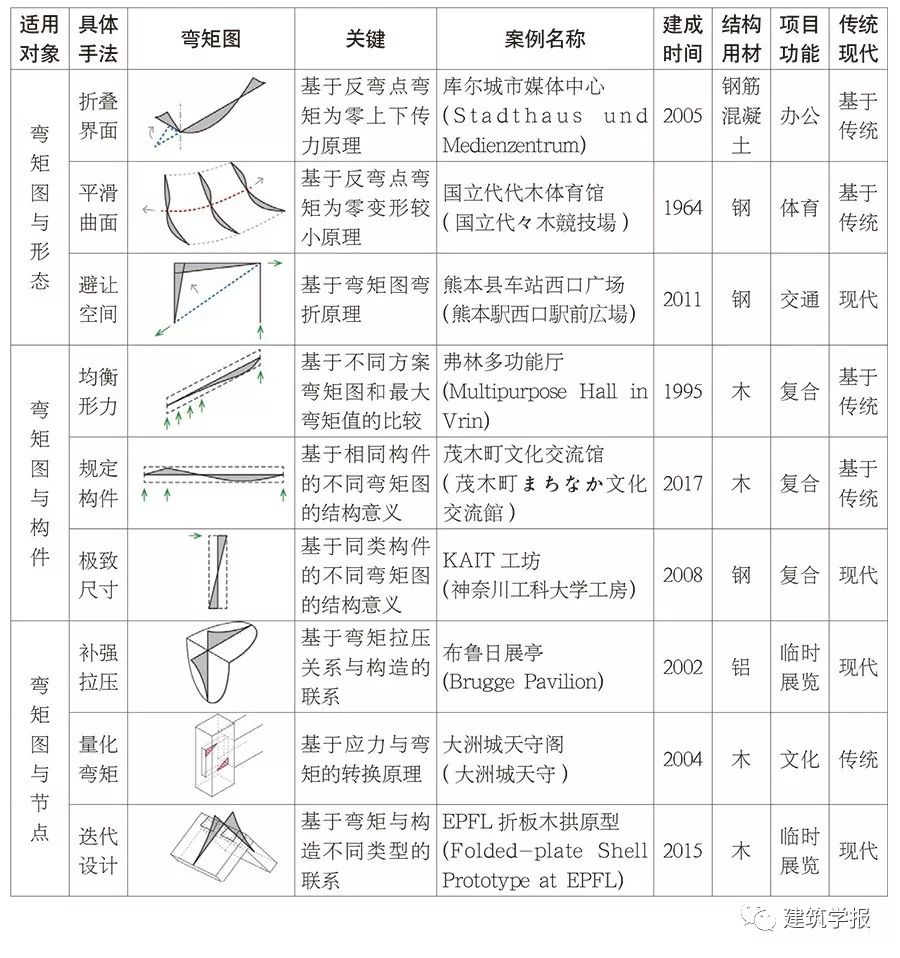
如表1所示,本文從建築形態到結構構件、再到構造節點,借助不同結構用材、不同建築功能、不限於現代或傳統的案例展開詳細分析,以多重角度和相對廣泛的適用範圍為建築師提供了基於彎矩圖的建築設計方法。